流体在离心风机中获得能量的过程,就是在叶轮作用下流体本身速度大小和方向变化的过程,这些工作主要在叶轮内完成,因此风机的叶轮对风机的性能起着至关重要的作用,直接决定了性能的高低、效率的大小。
离心风机中流体在叶轮中的运动和速度三角形是理解其工作原理的关键,也是风机设计的基础。
1. 流体在叶轮中的运动
流体进入叶轮后,主要经历以下运动:
轴向进入:流体沿轴向进入叶轮,所有离心风机的气流都是沿着风机的轴向进入叶轮。
径向流出:在叶轮旋转作用下,流体被加速并沿径向流出。
旋转运动:叶轮旋转带动流体旋转,形成复杂的流动。
因此,流体在离心风机叶轮中的流动是三维方向的,即轴向、径向、圆周方向,如下图所示:
2. 速度三角形
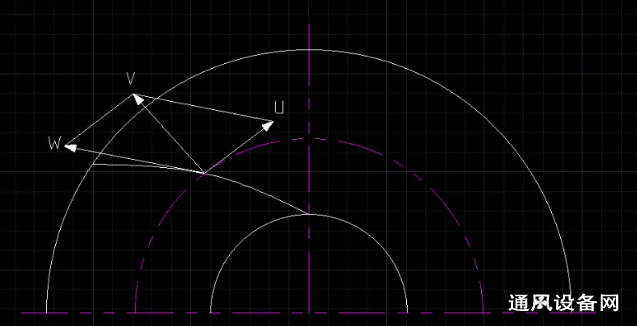
按照上面介绍的流体的运动是三个方向的,既有圆周运动,又有相对运动,可以采用速度三角形来表示,速度三角形用于描述流体在叶轮中的速度变化,主要包括三个速度分量:
绝对速度 (V):流体相对于静止坐标系的速度,即流体相对于蜗壳的绝对运动。
相对速度 (W):流体相对于旋转叶轮的速度。
圆周速度 (U):叶轮圆周上某点的线速度。
绝对速度V等于相对速度W与圆周速度U的矢量和,即:
V=W+U
对于离心风机叶轮内的任意位置,都可以画出上述的速度三角形。
对于风机入口,速度三角形用下标1来表示,即V₁、W1、U1。对于风机出口,速度三角形用下标2来表示,即V2、W2、U2。
3. 速度三角形的应用
速度三角形用于分析流体在叶轮中的能量转换,可以用来帮助计算:
理论扬程:通过欧拉方程计算。
效率:评估能量损失。
设计优化:改进叶轮几何形状以提高性能。
欧拉方程:
通过速度三角形,并假定流体为理想流体,流体在流道内处于稳定状态,可以推导出欧拉方程,欧拉方程描述了流体通过叶轮时的能量变化:

其中:





